线程
线程(thread)和进程(process)都是并发计算中的重要工具。其和程序(program)的基本关系形如:
- 一个程序可以有多个进程,一个进程可以有多个线程;
- 线程是进程的执行单元,每个进程至少有一个主线程,线程不能脱离进程而存在。
从资源分配(CPU、文件描述符、内存等)上看:
- 进程是操作系统分配资源的基本单位,不同进程间不会相互干扰;
- 线程则只拥有最基本资源(栈、寄存器等),同一进程内的不同线程共享堆内存和其它系统资源。
进行并发计算时利用线程的优势在于:线程极易被创建、销毁、切换和被调度,可以最大化对CPU多核的利用率。
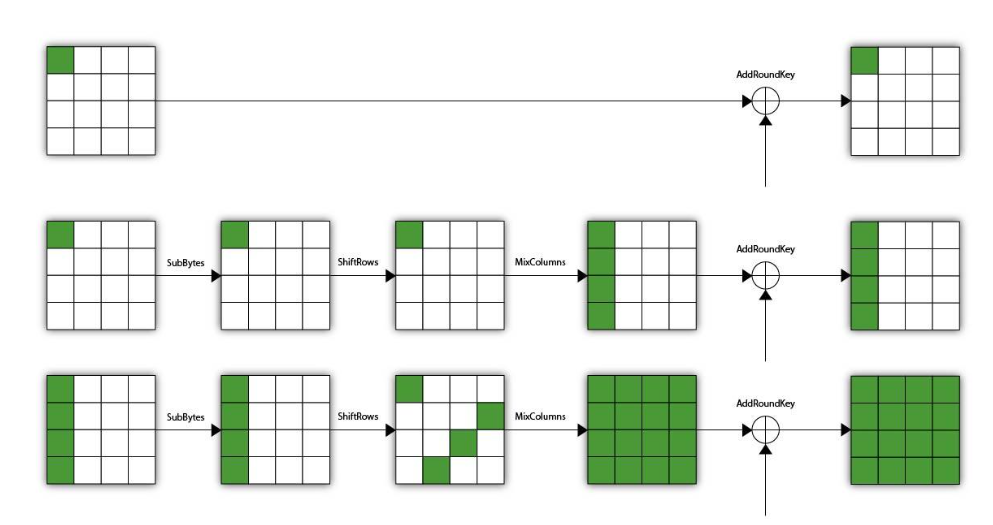
C++中的线程可分为四种状态:等待、活动、休眠、结束。
- 非空线程被创建后立即进入待执行队列
不像某语言非得,处于等待状态;implements不说还得run()一下(bushi)
- 当CPU有空余资源时,待执行队列中的线程会依次开始执行,进入活动状态;
- 线程在执行过程中可以主动地进入休眠(
sleep_for(...)/sleep_until(...))或等待(yield())状态。休眠状态下的进程一段时间后/达到某个条件后会被“唤醒”,重新进入等待状态,新进入等待状态的线程也会自动加入待执行队列;
- 线程代表的函数执行完成后则进入结束状态。
std::thread
C++标准的宗旨在于 standardizing existing best practice,其例之一即为
std::thread。
C++11前确实存在实现多线程的方法——现在几乎无人问津,亦不推荐使用的pthread库。当然如果读者认为线程句柄乱窜+函数指针满天飞的C样式老爷车编程非常好玩的话,不妨一试(doge),此处不再赘述pthread库的有关资料。
简介
C++11中,标准库<thread>引入的std::thread提供了跨平台、面向对象的、语义统一的多线程支持。
thread类
每个非空线程的本质都是一个函数,故thread的构造必以调用函数为基础。
重要成员函数
thread() noexcept;:默认构造函数,创建空线程
thread(Fn&& fn,Args&&... args);:以std::invoke(std::forward<Fn>(fn),std::forward<Args>(args)...)开启一个非空线程
~thread() noexcept:析构函数
thread(const thread&) = delete;复制构造函数(已显式删除= delete;)
thread(thread&&) noexcept:移动构造函数,调用后原thread将被置空
复制/移动赋值运算符与相应构造函数类似。
关于
std::invoke:其存在意义是统一C++中三种主流的函数调用方式:函数指针(function pointer)、函数成员指针(pointer to member function)、可调用对象(callable objects),因为三者的调用语法并不相同。又是一个新坑,哈哈
static unsigned hardware_concurrency():一个DETERMINSTIC的函数,获得当前程序运行环境的并发资源数
static std::thread::id get_id():获得当前thread的编号(id),其以一个嵌套类std::thread::id的形式给出
“并发资源数”指操作系统允许的能够同时运行的计算单元总数,多数情况下其与CPU的逻辑处理器数一致。
类id没有任何(接口式的)成员函数,其唯一用法是bool std::operator==(std::thread::id,std::thread::id)校验两个既得的thread标识符是否相同。
void join()、void detach()、bool joinable() const见下。
join/detach
C++中,thread的重要特性之一为其是否"joinable"(可以“加入”/“归并”)。
每个管理着一个线程句柄(thread
handle)的thread对象都是joinable的。
简明起见,本标题下接下来描述一个线程是否joinable时直接用
true/false简写之。
显然所有新创建的非空线程状态都是true,空线程则为false;对于状态true的线程对象,可以令其join()/detach()。其中,
join()后调用者将被阻塞(block execution),等待该thread代表线程执行结束后,调用者恢复运行。
detach()后该子线程将从对象中“解离”并令其自由执行(不再受同级线程约束),该thread置空。
可以认为,若将线程开始运行比作放飞风筝,
join()对应调用者等待风筝落地(此间操作者什么也不做),detach()则为剪断“风筝线”。
尽管C++的<thread>并未直接提供对线程进行更为底层操作的函数(比如强行让渡、休眠以至终止一个线程),但通过get_id获得底层句柄后,主线程在子线程未detach()时仍然具备控制之的“潜力”(如强行使其休眠、终止运行等);但调用detach()后主线程就无法再“控制”该线程了(此时主线程和该线程的地位是“平等”的,想要终止其运行等只能由更上层的OS调度实现)。
从线程句柄的角度来理解:
C++中每个线程在join()/detach()后该thread对象就会被置空,状态自然变为false(故thread是否储存了一个线程句柄是其状态为true的充要条件)。
join()相当于“使用”了这个线程句柄,使用完后即弃置之;detach()等价于主动抛弃这个线程句柄。
由于线程句柄显然只能移动而不能复制,故thread对象被移动后,原thread自然也不再拥有任何句柄,状态置false。
需要留意的是,是否拥有线程句柄和线程是否执行完成无关,线程即使未执行完成,其句柄也可以通过
detach()主动丢弃;即使执行完成,其句柄依然有效。
同时为了防止线程句柄泄露,C++中thread对象在析构时会校验其是否依然管理一个线程句柄。若其状态为true(相当于该thread从未join()/detach()过),则会在声明为noexcept的析构函数中抛出一个异常(翻译过来就是调用std::terminate,进而abort()终止程序)。
namespace this_thread
C++11同时引入了std::this_thread命名空间,其中定义了四个与多线程控制有关的函数。
void yield():当前线程“让渡”自身的CPU资源,主动进入等待状态。
void sleep_for(const std::chrono::duration<R,P>&):当前线程休眠一段时间。
void sleep_until(const std::chrono::time_point<R,P>&):当前线程休眠直至某时间点。
std::thread::id get_id():获得该线程的id供比较。
锁
进程间的资源访问由操作系统调度,且两个进程的资源隔离性强(即运行时,一个进程几乎不会和另一个进程产生资源冲突)。
相对之下,不同线程间的资源共享程度极高(尤其在对内存的访问上),若对它们的数据读写不加以控制,则极易产生“数据竞争”(data
race)这一现象。
数据竞争:当多个线程试图在同一时间读写某一片数据时,对于某些原子操作其未规定双方进行的先后顺序,继而导致程序的运行流程、输出结果不确定,甚至可能因内存访问冲突而导致程序崩溃的情况。
比如下述的代码就极易引发数据竞争,导致未定义行为(UB):
2
3
4
5
6
7
8
auto fn = [&](int x){vc.push_back(x);};
std::array<std::thread,10> th;
for(int i=0;i<10;++i)
{
th = std::thread{fn,i};
}
常见容易引发访问冲突的“资源”包括:文件流(file stream)、堆内存(heap memory)等。
互斥锁
C++11中引入了std::mutex,作为“互斥锁”来保证进程间执行的安全。mutex之名为
mutal exclusion,即“独占互斥量”的缩写。
std::mutex只有一个默认(无参)构造函数,mutex对象是不可复制/移动的(四个复制/移动相关函数/运算符全部= delete;);析构函数是平凡(trivial)的。
其public成员函数只有三个:
void lock():获得该互斥锁。若该锁已经被锁定,则本函数将阻塞线程执行直至成功获得该锁。“阻塞执行”这一行为是避免访问可能带访问冲突的资源、函数等时的关键:
1
2
3
4
5
6
7
8std::stack<int> stk;
std::mutex mt;
void push(int x)
{
mt.lock();
stk.push(x);
mt.unlock();
}如此做方能保证
stk同一时间只有一个线程对之进行操作,防止对同一个内存位置同时读写造成UB。可以发现
std::mutex一般会被设为全局变量,或以引用方式传入函数参数。void unlock():解锁。其和lock()操作应当“成对”出现,某线程若锁定了一个mutex,亦必须在退出前解锁之,否则将会造成死锁(deadlock)。
bool try_lock():尝试锁定(不阻塞线程执行),若锁定成功则返回true,否则返回false。
一些有关锁的概念:
死锁(deadlock):因各种原因导致一个获得lock的操作无法完成的情况。常见有两种原因:一个线程尝试连续两次锁定一个锁(lock()后再lock()一次,本质上是UB,当然大多数C++标准库实现中,debug下都会选择抛出一个带提示信息的异常);一个线程获得锁后没有解锁就退出(忘记unlock()、抛出异常、提早return)。
“呼应”操作(synchorized operations):两个应当“成对”出现的操作,比如new对应delete、lock()对应unlock()、fopen对应fclose等。几乎所有动态“管理”资源的操作 都应当是“呼应”的,即两个操作应当在某个操作周期内成对出现,否则会造成资源泄露(内存泄漏、死锁、文件标识符丢失等)。
一些容易导致“死锁”的反面示例形如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25std::mutex mt;
void bad_fn()
{
mt.lock();
if(???)
{
mt.lock(); //Repeated locks: UB, the program may deadlock
}
if(???)
{
return; //Early return, the mutex is never released
}
switch(???)
{
case ???:
throw std::runtime_error{""}; //Early return, the mutex is never released
/*...*/
}
mt.unlock(); //Only when the program reaches this point, the mutex is released
//If somehow this line is disregarded, the mutex is never released
}
御守:std::lock_guard
std::mutex在应用中极易出差错,故恰若对内存的管理有智能指针,对mutex的管理也有lock_guard这个包装类辅助之。
这些类的实现都是RAII(Resource Acquisition Is Initialization)原则的生动实践。
lock_guard实际上是一个类模板,除构造和析构函数外没有其它公有成员函数。
其作用只是“代理”一个mutex,在析构函数中自动解锁,构造时自动锁定(可选)。其设计简单而精妙,利用析构函数的特性成功规避了大部分
early return 导致的“死锁”情况:
1 | std::mutex mt; |
如果不希望lock_guard构造时锁定一次,可以构造时传一个
tag-type
的第二参数std::adopt_lock进行重载决议:
1 | std::lock_guard lg{mt,std::adopt_lock}; //Manages mutex `mt` yet does not lock it(assumes it has been locked) |
同样地,
lock_guard依然不可移动或复制。
咕咕咕:什么时候讲讲unique_lock和shared_lock
<future>
“异步”亦趋:std::async
C++中创建一个异步函数使用std::async函数实现。
std::async相比std::thread(非空构造)的特点之一在于,其通过一个(可选的)第一参数为std::launch的重载来实现可选的“手动调度”:
1 | void f(); |
因此当我们需要延迟一个线程生命周期的开始(或显式地指出这个线程的生命周期将立即开始)时,就可以传入std::launch::deferred/std::launch::async作为第一参数(实际上enum class std::launch也只有这两个选项)。
std::async的返回值是类模板std::future的一个实例。但std::future又为何物?其又何以操控线程生命周期何时开始?稍安勿躁,且听下回分解
逆料其事:std::future
在讲解std::future前,先引入我们并发/异步编程中的一个重要动机:获取子线程执行结果(返回值)。
在cppreference中对thread对象的介绍中,有一句描述值得玩味:
The return value of the top-level function is ignored and if it
terminates by throwing an exception, std::terminate is called.
即,用于构建thread的最顶层函数的返回值将被忽略,且其亦被隐式的禁用了栈回溯(stack
rewinding)(异常逃逸后直接调用std::terminate)。
相较普通的函数调用,其自然引出了两个问题:
- 函数返回运行结果最重要的方式之一——返回值,如何在并发/异步编程中实现?
- 线程执行仍应有异常处理,不能
throw的情况下何以让上层函数知晓?
std::future给出了前者的答案,其包装类std::promise则回答了后者。
此情可待成追忆,只是当时已惘然。
std::future是一个颇为有趣的类模板,其主模板只接受单个类型参数Ty(两个模板特化分别是void和Ty&)。
线程放出多个子线程进行异步/并发工作时,其知道子线程会返回某个值(比如获取用户输入函数的std::string,某加密函数的std::array<byte,16>等点名AES-128),但在“放出”该子线程时还没有这个值——只知道子线程会在未来的某个时间点返回之。
由此出现了std::future的概念,std::async以返回T的函数创建线程时,返回值类型就是std::future<T>。
常用成员函数
bool valid() const,返回一个std::future对象是否有效。每个非空构造(代表了一个异步线程)的std::future对象构造时都是有效的,但调用get()后其就失效了(且不可恢复)。
Ty get(),调用后其会阻塞程序执行,等待子线程完成并获取其返回结果。显然其返回值类型和底层返回值类型一致;只有有效的(valid())的std::future才能调用get()方法——等价于get()也只能调用一次。
void wait() const,调用后其会阻塞程序执行,等待子线程完成,但不会使线程失效,亦不提取其返回值。其同样只能对有效的对象上调用(否则抛异常)。
std::future_status wait_for(rep) const,和wait()区别在于若子线程在rep后依然未结束,则直接返回。
std::future_status wait_until(rep) const,类似地,等待直至rep后不论子线程是否结束,直接返回。
std::future_status是一个enum class,其可能取值有三:
deferred,代表该线程尚未开始执行;ready,代表该线程已执行结束;timeout,代表该线程截至wait_for/wait_until函数执行完成时尚未执行完毕。
故
std::async产生的异步线程就出现了一个诡异的函数美学:t.wait_for(std::chrono::miliseconds(0))(为什么不先)就可以检验一个子线程的执行状态。using namespace std::chrono_literals然后直接上0ms
当然此类函数美学在C++史上也不是第一次了,点名在C++23的部分wrapper_class加入前的vc.find(1) != vc.last()或者str.find(1) != str.npos
同时,std::future亦是可移动而不可复制的(复制构造函数和复制赋值运算符被声明为= delete;)。
现在还可以揭晓之前关于std::async“延迟起步”子线程的答案了:
对于第一参数为std::launch::deferred的线程,其会在其future对象调用get/wait[_for|_until]成员函数后开始运行。
若只想使之起步而不想阻塞程序执行,则可以搬出万能的t.wait_for(std::chrono::miliseconds(0));,随后再另行获取结果/其执行状态。
示例
1 |
|
山盟海誓:std::promise
std::future虽然在让线程“善始善终”方面迈出了一大步,但从线程执行过程中的“通信”来看,其依然稍显笨拙——状态的获取仅限于是否开始/结束,传递值亦只能在std::async构造的线程return时进行,且该值不能修改。
由此,出现了对异步机制更为适配的包装类std::promise。
特性
std::promise和std::future的模板参数赋法相同,通过get_future方法可以获得底层的std::future对象进行进一步操作。
作为包装类,其提供了相较std::future更强大的几个功能:
- 可以多次赋值,线程可以对
std::promise多次调用set_value(_at_thread_exit)成员函数来多次赋值/在线程退出时赋值。相较只能单次赋值且不可改变的std::future,显然其实现了线程间的动态通信更加灵活;
- 通过
set_exception(_at_thread_exit)成员函数可以设置将抛出的异常(通过赋予一个exception_ptr实现)。
示例
如,假设线程A正在等待线程B运行的结果,但它亦有自身的一些其它任务需要运行,此时可以在两个线程代表函数的形参中设置std::promise或std::future的引用用于线程间通信:
1 | using namespace std::chrono_literals; //0s |
结语
并发和异步编程是程序设计实践中的极重要课题之一;善用“”之术可以最大地让程序的执行更贴近现实中事物的运行逻辑,极大地提高程序运行效率,并符合程序在实际应用时的业务逻辑要求。
因此,C++11引入的“山珍海味”实际上只是开胃菜——其只是拉开了现代C++帷幕,后继的C++版本都在并发/异步编程上有许多大动作,包括C++20四大金刚之一的coroutines,皆在尽可能提高并发/异步编程的效率、可靠性、功能性与易用性。