简介
在深圳奥联信息安全有限公司实习期间,开发Cryptool2插件的一些小记。
Cryptool2介绍
Cryptool2是一款开源软件,其内置了大量密码算法的“图形化编程”插件,通过不同输入/输出相连接,可极为直观地展现密码算法内部/密码应用中不同函数的调用流程。
其内置了极大量密码学算法插件(涵盖古典密码学的各种奇技淫巧,现代密码学中经典的对称加密、非对称加密、数字签名、哈希函数等),同时用户也可自行开发插件并应用之。
由于其插件封装后的图形化流程设计非常生动形象,故其最大的用武之地之一即为新标准的教学与演示用途:
主要工作内容
根据GM/T 0018-2023:密码设备应用接口规范在Cryptool2中实现对应函数的插件,并基于新开发插件完成SM9密钥协商、加解密、签名与验证等的全流程demo。
最终实现节选(SM9密钥协商):
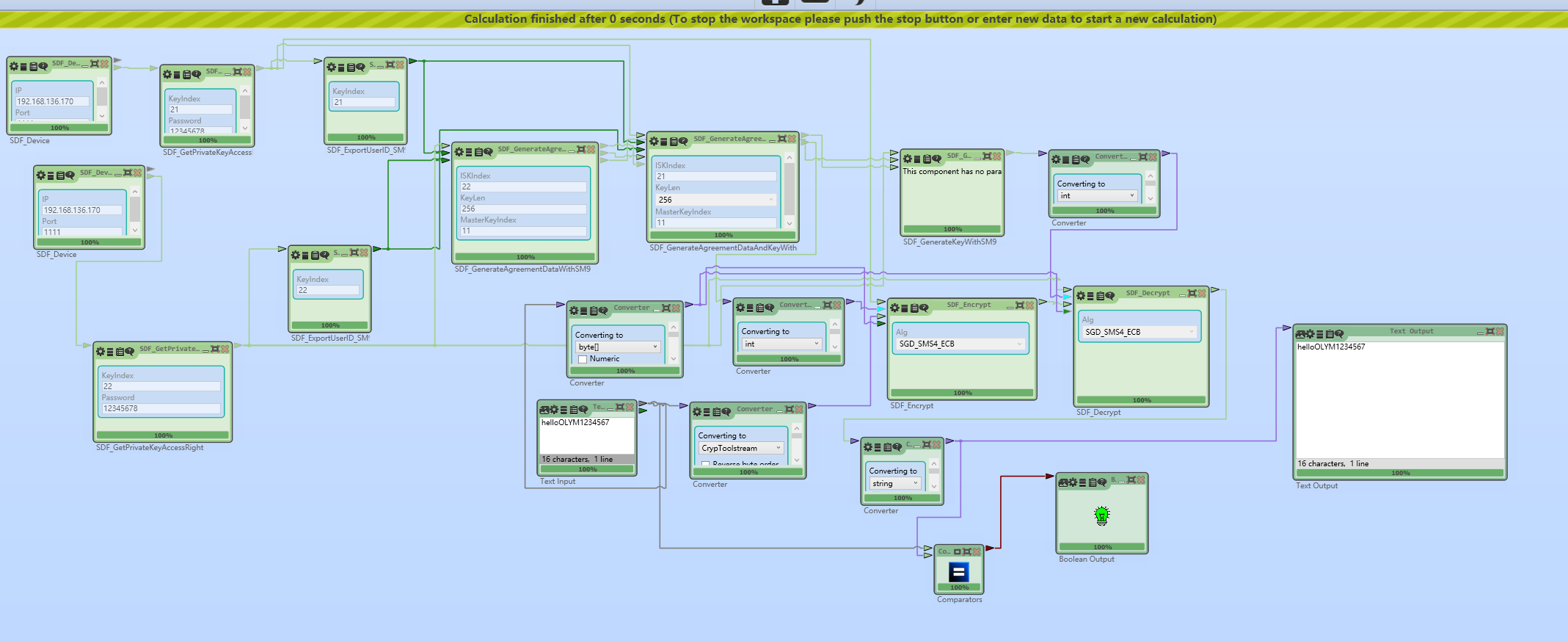
浅析
Cryptool2是.NET架构下的软件,其插件的“特性”都可以在C#代码中找到:
- 具有任意数目的输入/输出端接口供连接,数据类型可自定义
- 通过
Settings可以接收外部输入“设置”型参数,支持多种选择方式(如文本框TextBox、复选框ComboBox等)
- 可以展示内部的运算流程(较高级)和计算进度
- 通过
OnPropertyChanged可以让某个输入/输出参数发生变化时“知会”连接的关联端口,再发起一次计算
技术栈
- 密码学基础及应用知识(加解密、签名与验签、密钥协商、散列函数应用、国密算法等)
- 服务器密码机接口封装调用
- C++和C#语言程序设计、C#中调用C++函数的逻辑
- 基于Visual Studio 2022进行大型项目开发
部分技术详解
dll调用
DLL,全称Dynamic Link
Library(动态链接库),表示程序在编译时只保留了某个“外部”函数的入口,运行时从另一个动态链接库文件(Win下的.dll,*ix下的.so)调用之。
如此做的优点包括但不限于:
- 允许跨语言调用(如C#调用C++代码)
- 减小主程序体积
- 通过DLL复用(多个线程/进程可以多次调用同一个DLL且互不冲突)来降低空间占用
- 拓展功能时不需要重新编译整个程序或变动既有基础架构
如在CrypTool2插件的开发中,每个插件的子项目的编译结果都是.dll,如此在新建/变更组件时不需要重新build整个项目,只需(重新)编译该项目对应的dll即可。
在密码学应用中,运行效率至上的原则决定了其底层密码算法最好用C/C++实现——故在编写好C++代码逻辑后,从C#中调用C++代码也就成了完成“夹心”的关键一步。
C#中通过DllImport属性声明可以发起一次对外部dll的调用,如:
1 | [] |
其中由于C#和C++堪称隔行如隔山明明都是++,为什么C++和C的差别还没这么抽象,因此调用中有诸多关键点:
- 首先数据类型必须一致(基本数据类型外,结构体等还需要
MarshalAs和StructLayout等显式明确其内存排列方式,否则出错几近于必然事件);
- 由于C++和C#对底层数据的处理方式不同(如C#中除不安全代码外没有“指针”的概念,与C++指针和引用泾渭分明相对),因此在传参时应当进行一些“翻译”。
如,根据GM/T
0018-2023,上述SDF_GenerateAgreementDataWithSM9函数的C语言原型如下:
1 | int SDF_GenerateAgreementDataWithSM9( |
其中HANDLE是void*的typedef,BYTE为unsigned char,ULONG为unsigned long。
将之“翻译”为C#的extern函数声明时的注意点有几点:
- 基本类型(含指针,对应C#
传奇般的IntPtr)可以直接传参;
- 带有指针/引用性质的传参时,需留意其功能上的属性为输入还是输出量。解法有三种:
ref,对应C/C++的一阶指针/引用(输入/输出);out,用于输出变量(从C#的角度看可以内联变量声明,C/C++中依然是使用指针/引用传参);做数组“提升一维”,形如C#的int[]对应C++的int*。
使用
out进行传参时部分场景下容易出现运行错误,原因不明;其或与out内联变量的内存初始化时机有关(尽管out的“函数内初始化”更应偏向语义约束,栈内存应在进入函数前就已经分配完成),故使用int[1]类似的传参方式依然最为稳妥。
如存在C++函数:
1 | int nihao(const int* read,int* write); |
对应C#的外部调用方式可以形如:
1 | [] |
调用时,由于C#要求关键字“二次确认”(即调用时、声明时需要同时声明关键字out/ref等),故上下文可能形如:
1 | public void func() |
Property相关
输入/输出数据方面,只需要在类中声明一个Property并明确其属性,期望的数据类型即为Property自身的类型,get和set方法均为默认值。
如这段代码:
1 | [] |
效果形如:

其中最后一个参数仅在性质为Direction.InputData时有效,表示该输入是否为必须值(若未输入则该插件不运行,否则以缺省值运行)。
这些Property在管理上的另一个显著特征为:改变其值后,应当调用OnPropertyChanged函数来“告知”与之相连的模块此Property更新了数值,达成宏观上“流水线”般工作的效果:
1 | if (iRet == XCipherEngine.SDR_OK) |
Settings同样也采用Property的方式表述,其和输入/输出数据的差分只在于set函数和私有变量的“另行”设置。参考:
1 | private uint iskIndex = 0; |
其动机依然在于关键的OnPropertyChanged——识别新的设置项是否与以往的不同,若然,则触发新一轮计算。
显然这种get和原变量分离的方法也可用于其它逻辑的封装,如:
1 |
|
