AES积分攻击——霜天

2025-05-22

书接上回...

上述我们讨论了当我们能够获得一个（最好是多个）delta-set 时的攻击方法。那么，假如受制于攻击条件等（如上述的加密Orcale只给了100次“随机”加密机会，最终获得的不同密文甚至可能只有60-70个），无法获得这样的 delta-set 呢？

回顾

柳暗花明

逻辑推理中，即使事件A是事件B的充分而非必要条件，只要假阳性(false positive)概率足够小，依然可以认为从事件B可以推导出事件A。
而密码分析亦然，我们所需做的就是从这个非完整的密文集（Δ'-集）中，找出可被如此利用的性质。

回顾我们有关“活跃位置”的分析图：~~不知道不同色块什么意思的赶紧去翻“启卷”(4-1)章，笑~~

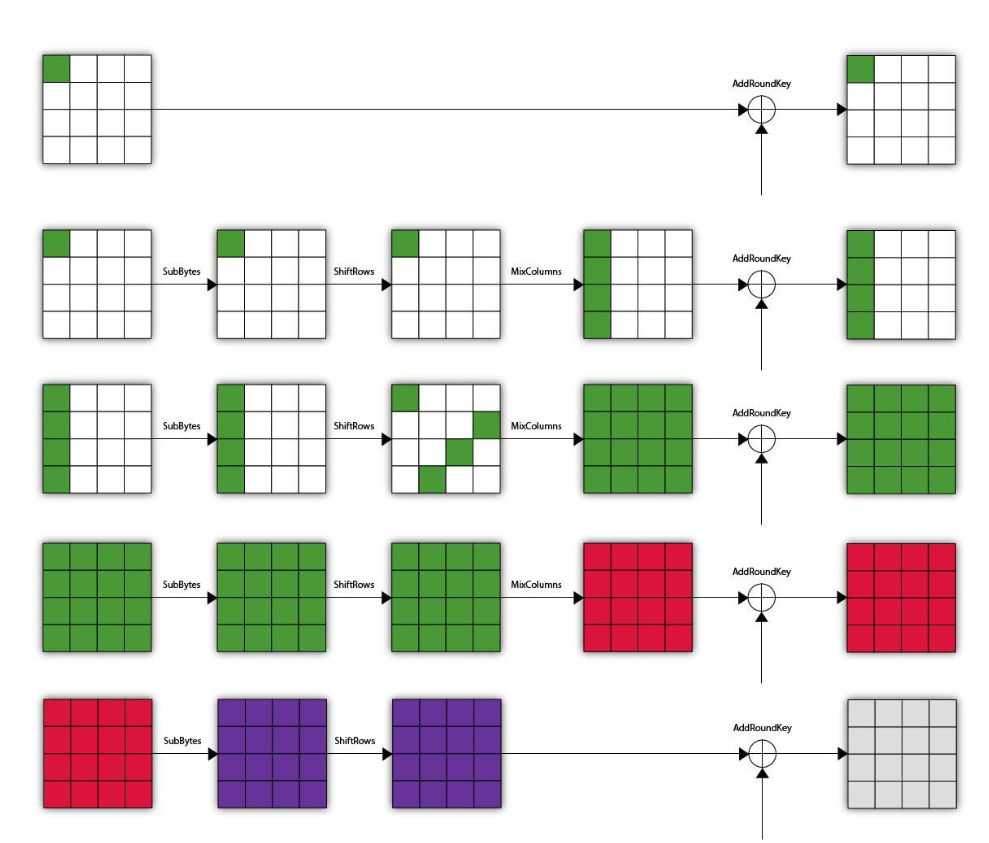
相较Δ-集，Δ'-集的不同之处在于红色位置失去了“归元”的特性。

在Δ-集中，对于0-255中的每个值，活跃位置（绿色色块）会遍历且只会遍历一次。
相应地，对于Δ'-集，虽然活跃位置不能遍历全部的值，但对于同一状态下的Δ'-集，同一个活跃位置的取值必定是不重复的。

由上述这张图，可见只要将密文回退至第三轮的逆列混淆(InvMixColumns)前，验证该组密文是否具备该特性，即可——至少理论上，“筛选”出可能正确的密钥。

正向分析

将时间拉回到第三轮的列混淆前，其后生成密文需要经历的步骤为：MixColumns -> AddRoundKey[3] -> SubBytes -> ShiftRows -> AddRoundKey[4]。
以追踪(0,0)这个活跃位置为例，
其在MixColumns后会受到第0列所有值的影响（参考gmul的“系数组”2,3,1,1），随后经过第三轮的AddRoundKey，相当于其“影响”扩散时，依赖的密钥有第三轮轮密钥的(0,0),(1,0),(2,0),(3,0)；
第四轮的SubBytes不会对位置追踪产生影响，而ShiftRows后，这四个位置会变成(0,0),(1,3),(2,2),(3,1)。
相当于我们从Δ'-集“倒退”至这个性质成立时，为了验证位置(0,0)的该性质是否成立，需要爆破的轮密钥的下标也和上述相对应，即需要第三轮的(0,0),(1,0),(2,0),(3,0)和第四轮的(0,0),(1,3),(2,2),(3,1)共计8个位置的密钥。
直观上，如此爆破需要 \(2^{8 \times 8} = 2^{64}\) 次枚举，计算上已经趋于不可行~~只比直接爆完整的128bit密钥好那么一点点~~。

逆向分析

同时，显然只依靠一个活跃位置的性质校验直觉上亦不够可靠。所幸，“反着来”我们可以发现，(0,0),(1,3),(2,2),(3,1)这四个位置的密文实际上可以被归纳为一组——它们都受到上述相同8个位置密钥的约束。

亦可认为这几个位置就是对单个活跃位置的一组密文，进行MixColumns+ShiftRows后四个位置“散开”的结果。

因此，在对密文性质进行检验时，可以将这些密文标记为相同“颜色”并在读取时即划为一组，并一次性校验4个位置是否均各自满足 回溯后取值两两不同 这一性质。
参考下述图片：

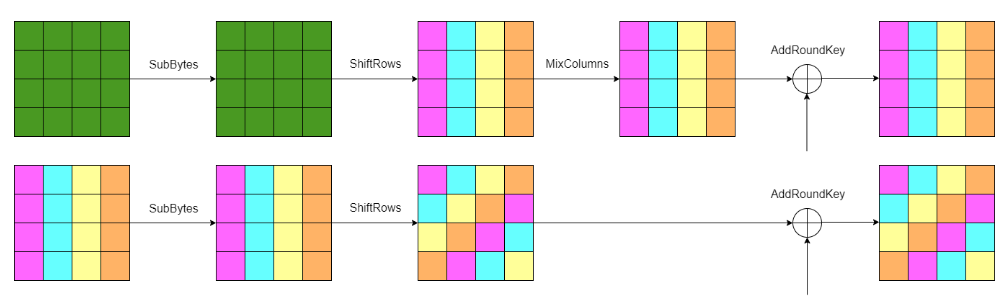
巧翎

啾啾————

至此这个攻击依然不具备计算可行性——单次依然需要同时爆破8个位置的轮密钥；同时AES密钥扩展函数的精心设计也最大程度地抵御了密钥分析攻击（使得这两部分待枚举之间可被利用的线性关系极弱）。

但得高人指点，我们实际上只需要爆破第4轮的密钥——亦即第3轮的轮密钥取值我们可以忽略（对解题无影响）。何以如此？

其原因在于我们待校验的密文集性质和第3轮的轮密钥无关。
虽然我们追踪单个位置时，其“扩散”到的目标位置的取值受到了第3轮轮密钥的影响；但由于我们试图校验的性质是回溯后密文集中，同一位置取值不重复，对于同一位置而言，该轮密钥只是在结果密文中加上了一个固定偏移（尽管受到SubBytes、ShiftRows的影响，其映射的下标并不是直观上的“下标”，且偏移量并不等于该位置的轮密钥值），并不会影响上述待校验的性质。
换言之，在我们执行“回溯”操作时，进行到第3轮的AddRoundKey时可以随意填一组轮密钥，继续进行——简便起见，直接填全00（即什么都不做）即可。

因而，我们的爆破对象也被约束到了第4轮同一“颜色”的密钥，即只需要对4组密钥分别进行至多 \(2^{32}\) 次爆破，初步具备了计算上的可行性。

攻击

由于爆破的计算量依然极大，故考虑采用C++代替Python实现该攻击。

C++的优势包括但不限于：多线程的更原生和更适配的支持、对称加密体制中更为“得心应手”、-O3//Ox优化拉满的极限突破、“手动挡”内存管理节约的大量虚拟机/垃圾回收开销等。

宏观分析

核心组件包括：

待爆破密钥集的生成、分组函数，多线程调度；
对密文进行分组（按“颜色”区分之），由于每组密文的字(word)密钥间是独立的，故对每组密文的所有可能密钥字组合进行回溯，并验证是否符合该性质。

其中，第二步回溯涉及到的AES组件包括 AddRoundKey[4] -> InvShitRows -> InvSubBytes -> AddRoundKey[3] -> InvMixColumns。
由于第3轮的轮密钥对性质验证没有影响，故对其密钥值取全0以略去之；
同时第一次InvShiftRows也可以通过下标“打表”的方式，在密文读取阶段即对之进行分组（除能节省 \(2^{32}\) 次重复操作外，另一个优点是和第4轮的密钥下标分组同步）。

微观实现

Github等在线资源中不乏既有的AES加密类、积分攻击函数（包括Δ'-集攻击）的C++实现，但~~出于Modern C++强迫症和无所事事等原因~~笔者依然选择了从头手搓整个AES组件。
主要动机在于充分利用现代C++的各种特性，在保证效率最大化时，相较既有的C-Style或传统C++实现，最终代码具有更好的扩展性、可读性和可维护性~~不用注释就能讲明白那种~~；
同时在类型安全、边界安全等更贴近实践应用的课题上更上一层楼。

类型安全的一个最直接的实例无疑就是byte的实现问题。虽然byte的范围确与unsigned char应一致（0-255），但若直接使用后者作为密文的数据类型，则从代码维护的角度来说无疑是竭泽而渔之举——为后续的类型安全问题和无尽的bug埋下了伏笔。

C++中很多“冗余”的语法特性、编译期约束等的目的并不在于提高效率——恰如其反，若编译器的优化欠佳或代码质量堪忧，则最终程序在效率上甚至会有较可观的损失。
作为一门广泛应用于大型程序开发的语言，其要素在于通过大量的静态检查、语义约束来“防患于未然”，将尽可能多的问题提前至编译期发现并解决，避免在运行时debug太多问题弄的人头皮发麻~~Python的很多函数调用有感~~

`byte`？

C++17中标准库确实引入了std::byte这一enum class，其在类型安全等方面确实有所建树，但enum class拒绝了所有隐式类型转换的特性依然使其在应用上有诸多不便~~谁想天天std::to_underlying和static_cast呐~~，其配套的函数组件也仅限于namespace std里的“半截子”operator???(byte,byte)重载支持。

考虑到AES中对byte类的需求，最终“手搓”的struct byte形如：

struct byte 
{
    explicit constexpr byte(unsigned char _val) : value{_val} {}
    constexpr byte() : byte(0) {}

    // Default special member functions
    constexpr byte(const byte&) = default;
    constexpr byte(byte&&) noexcept = default;
    constexpr byte& operator=(const byte&) = default;
    constexpr byte& operator=(byte&&) noexcept = default;
    constexpr ~byte() = default;

    // Conversion
    constexpr operator unsigned char() const noexcept { return value; }

    // Bitwise operators
    friend constexpr byte operator&(byte x, byte y) noexcept
    {
        return byte{ uc(x.value & y.value) };
    }

    // Compound assignments
    constexpr byte& operator^=(byte right) noexcept
    {
        value ^= right.value;
        return *this;
    }
    friend constexpr byte operator^(byte x, byte y) noexcept
    {
        return byte{ uc(x.value ^ y.value) };
    }

    friend constexpr byte operator|(byte x, byte y) noexcept
    {
        return byte{ uc(x.value | y.value) };
    }

    friend constexpr byte operator>>(byte x, byte y) noexcept
    {
        return byte{ uc(x.value >> y) };
    }

    friend constexpr byte operator<<(byte x, byte y) noexcept
    {
        return byte{ uc(x.value << y) };
    }

    //compound assignment operators

    constexpr byte& operator&=(byte right) noexcept
    {
        value &= right.value;
        return *this;
    }

    constexpr byte& operator|=(byte right) noexcept
    {
        value |= right.value;
        return *this;
    }

    constexpr byte& operator>>=(unsigned char shift) noexcept
    {
        value >>= shift;
        return *this;
    }

    constexpr byte& operator<<=(unsigned char shift) noexcept
    {
        value <<= shift;
        value &= 0xff;
        return *this;
    }

    // Comparison
    friend constexpr auto operator<=>(const byte&, const byte&) noexcept = default;

    // Literal operator
    friend constexpr byte operator""_t(unsigned long long) noexcept;

    unsigned char value;
};

笔者在实践中发现的一些“妙手”如下”：

最初考虑到类型安全，对struct byte的构造函数（相当于“进”）和转换构造函数（“出”）都采用了explicit修饰之；但如此发现在应用中又会需要用到大量的显式cast。
如此做既牺牲了大量可读性（即使不用static_cast之类，函数式转换堆砌也有过度冗余之病），同时严格来说亦降低了维护性（无法便捷地修改上层实现，参考即使是在非模板函数中，using指令依然大量存在，抽象底层实现的动机）。

最终经过多番测试研究，决定采用单向explicit便于配套组件的实现和实践应用：byte的构造函数被标记为explicit，但其转换构造函数（operator unsigned char）则没有。

结合operator ""_t(unsigned long long)，其能够达成的实现效果形如（以gmul配套函数的实现为例）：

constexpr byte gmul_fn(byte a, uc b) noexcept
{
    byte p{};
    while (b)
    {
        if (b & 1)
        {
            p ^= a;
        }
        byte hi_bit{ a & 0x80_t };
        a <<= 1;
        if (hi_bit)
        {
            a ^= 0x1b_t;
        }
        b >>= 1;
    }
    return p;
}

（注释：using uc = unsigned char;）

单向explicit的具体动机包括：

由于只定义了byte和byte之间的三种位操作(|、&、^)，同时亦不希望unsigned char乱掺和，故选择将byte的构造函数声明为explicit，避免胡乱按位操作返回byte的情况发生，同时通过字面量运算符保留了常量向byte的高可读性表示；
operator unsigned char使得byte类不需要什么std::to_underlying/static_cast就可以提取其底层数据类型，在能够进一步“搭桥”转化为bool提高应用便利性的同时，不会影响byte对象自身的数据安全。

同时，struct byte的按位与/或/异或操作的两个操作数都是byte，但operator<<=和operator>>=的右操作数最终被定为了unsigned char。
笔者如此做的动机是此处没有必要设定byte的类型约束（大于8的移位数都会让byte置零），反而牺牲了明确的可读性。
若仅考虑AES的gmul“打表”等编译期固定移位数的场景，确有迂回之方法——利用consteval实现字面量约束（参考C++中对operator<=>(std::strong_ordering,???)约束右操作数必须为字面量零(Literal zero，即一个裸露的0)的约束方法实现）。

攻击部分概览

核心部分是是verify函数（即校验一个给定密钥对于某个分组的密文是否正确）。

注释：存在typedef形如using word = std::array<byte,4>;和using cipher_group_rvw = std::span<const word>;。

其中由于密文已经被预处理+分组过（按颜色分段），故在“回溯”时亦只需进行AddRoundKey（第4轮）、InvSubBytes（第4轮）、InvMixColumns（第3轮）三次操作即可开始校验。
当然如此解出来的第4轮轮密钥亦是被“分段”的，后续会再行处理。

static constexpr bool verify(word partial_key,cipher_group_rvw vws) noexcept 
//vws is the pre-processed(shift-row completed) ciphertext "identical-color" 4s
{
    using check_map = std::array<bool, 1024>;
    check_map mp{};

    for (word vw : vws)
    {
        bytes_xor(vw, partial_key);
        inv_sub_bytes(vw);
        inv_mix_columns(vw);
        for (auto idx : iota_word)
        {
            if (auto& position = mp[idx * 256 + vw[idx]];position)
            {
                return false;
            }
            else
            {
                position = true;
            }
        }
    }
    return true;
}

iota_word是std::views::iota(0,4)。

性能优化点小记

在校验是否满足两两不同的条件时，最初考虑易用性上了std::map<int,byte>，后续先是改为std::unordered_map，再改为bool数组。尽管bool[1024]确实稍有违背类型安全之理念，~~但架不住它不需要像几个map那样扯皮~~。（若稍微牺牲少量效率，是否还是可以将之封装，校验时以operator()的方式调用，兴许在可读性上能取得更好的效果？）
线程调度上，最初采用并行组爆破（即4组密钥分别交由4“组”线程进行爆破），后续考虑到应尽可能减少线程空置时间，故在密钥组攻击上采取“逐个击破”的方法，即令所有线程验证同一组密文集的“回溯”结果，每个thread会在密钥第1位固定下爆破剩余 \(2^{24}\) 个密钥。

语义优化点小记

gmul的表最初选择生成后直接贴成字面量数组，后续改成了consteval函数打表，如此能实现极高的维护性和可读性~~想必谁看到一个byte[2048]都是懵的~~且完全不影响运行效率。
struct byte的诸多实现，见上。
大量摒弃了传统的for循环，全部改为 range-based for。其中对于在容器上的操作，视情况采用传引用/传值；对于单纯遍历一个区段的数~~for i in range(256)这样~~，则采用了ranges库的std::views::iota组件代替传统循环。
> 其一，结合一些预定义的auto变量（如auto iota_word : std::views::iota(0,4)）能够~~舒缓一下审美疲劳~~让循环语义更为清晰、易于维护且不易出错；
其二，std::views::iota具有更类似于Python中range的特征（生成器式的惰性计算），语义上的优势在于循环体内部对i变量的操作并不会影响循环进行，具有更好的安全性和冗余度（甚至可以const修饰接收之变量，实现“固若金汤”的约束，而传统for循环显然无法如此做）；
其三，由上述点引申而来，由于循环次数（流程）是确定的，因而给了编译器大得多的优化空间，效率上亦可得到提升。
全篇除constexpr变量（等价于编译期常量）外不出现任何C样式数组（[]）、指针运算(pointer arthimetic)；采用std::array和std::vector作为容器类，协助托管内存和元素追加/删除等操作；视图上采用std::span明确归属、只读语义的前提下最大化效率（读写上经过std::span可以达到极接近原始指针的水平，远高于const std::vector&等），同时保证范围信息完整传递，极大降低段错误概率。

传送门

独立项目和完整代码实现：
Github: AES-Integrals

结语

书到用时方恨少，事非经过不知难。

密码学中绝大部分的实践，乃至很多突破性的探究的起点都在于此——或多或少地循前人之足迹。
但无论在何领域，“复现”中只要愿意下功夫、和自身既有知识结合起来，勤加思索探究，必然能有或大或小的突破，乃至在此领域豁然开朗。

这次实现攻击亦是如此：其中的主体攻击思路均参考了David Wong的blockbreakers和最初~~带我入坑~~的知乎解析。
能让笔者在这次攻击中收获颇丰的，除高人引路外，更多的是将自身现代C++编程理念的精进实践，以及对密码分析原理的深入理解与改进思考。

C++和密码学，二者求道之途尚漫而艰——此题或意在树一帜，稍记此“妙手偶得”之一瞬，更待来日朝花夕拾，继此小成所启之新篇。

回顾