AES积分攻击——云帆

2025-05-07

积分攻击简介

积分攻击(Integral Attack)是选择明文攻击(chosen plaintext attack)的一种，主要针对的是采用SPN(Substitution-Permutation Network，置换-扩展网络，以AES为代表)进行块加密的加密系统。

其核心思想在于：SPN中，某一位置的明文差分经过块加密的扩散过程会影响到许多位的密文，此过程可能使得某个中间量（加密部分轮数的密文）具有某种性质；
且再进行一轮加密后这种性质会因置换-扩展而被破坏，此时对该轮的轮密钥进行猜解，将密文集的状态回退到具有该性质的时刻，通过验证其性质是否仍成立来爆破密钥。

AES基本要素回顾

AES的主要组件包括SubBytes、ShiftRows、MixColumns、AddRoundKey。
其中AddRoundKey所用轮密钥由初始密钥“扩展”而来，且该扩展过程可逆。

密钥扩展

AES-128的密钥扩展是将初始密钥扩展至(加密轮数+1)组密钥的过程，初始密钥与轮密钥大小均为16字节。
密钥扩展是迭代算法，当前组密钥仅由上一组密钥决定：

前4字节为 上一组密钥的前4字节 与 上一组密钥的最后4字节的s_box置换值 对应异或；
将首字节再与 $GF(2^{8})$ 下的 $2^{i}$ 相加（也就是相异或，$i$ 为当前轮数）；
后12字节为 上一组密钥的前12字节 与 当前密钥的前12字节 对应异或（逐个进行）。

是不是感觉文字描述起来太别扭？那句编程界的名言还在不断发威—— Talk is cheap. Show me the code.

def key_expansion(init_key:bytes):
    rnd_key = [init_key]
    r_con = (0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80,0x1b,0x36) #2^n under GF(2^8)

    for i in range(1,rounds + 1):
        prv = rnd_key[-1]
        cur = []

        for j in range(4):
            cur[j] = prv[j] ^ s_box[prv[-j]]

        cur[0] ^= r_con[i]
        
        for j in range(4,16):
            cur[j] = prv[j] ^ cur[j-4]

        rnd_key.append(cur)

    return rnd_key

微观

SubBytes

这是AES中唯一的非线性变换步骤，其通过一个设计极为精巧的S盒(S-Box)实现。S-Box本质上是 $GF(2^{8})$ 下元素的双射。

对于给定的元素 $a \in GF(2^{8})$，计算其S-Box的对应元素过程如下：

计算 $GF(2^{8}) 下的 a^{-1}$（基于模不可约多项式 $x^8 + x^4 + x^3 + x + 1$ 进行，可利用扩展欧几里得算法/“查表”实现）；
将 $a^{-1}$ 扩展为 $GF(2)$ 下的向量 $v = (v_7,v_6,\cdots,v_0)$，计算 $v' = v \cdot M + c_0$，将结果向量 $v'$ 还原为 $GF(2^{8})$ 下的元素即为结果。

其中第二步应用的 $GF(2)$ 下的矩阵 $M = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\0 & 1 & 1 & 1 & 1 & 1 & 0 & 0 \\0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \end{bmatrix},c = \begin{bmatrix} 1 & 1 & 0 & 0 & 0 & 1 & 1 & 0 \end{bmatrix}$ 。

最终的S盒形如：

s_box = (
            0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
            0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
            0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
            0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
            0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
            0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
            0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
            0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
            0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
            0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
            0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
            0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
            0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
            0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
            0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
            0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16
        )

ShiftRows

“行移位”，AES的线性变换步骤之一，第 $i$ 行向左循环移位 $i$ 次。

注意AES块(block)中字节排布是列优先（而非多数矩阵计算的“惯例”行优先），因此在代码实现中看起来就像第 $i$ 列向上循环移位了 $i$ 次一样。

以Python代码演示之：

def shift_rows(ls):
    return [
    ls[0],ls[5],ls[10],ls[15],
    ls[4],ls[9],ls[14],ls[3],
    ls[8],ls[13],ls[2],ls[7],
    ls[12],ls[1],ls[6],ls[11]
    ]

若将原块视为 $GF(2^{8})$ 下的 $4 \times 4$ 矩阵，也可以认为其与给定矩阵 $M_{S}$ 进行了乘法（“线性变换”的本质），形如 $M_{S} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}$。

MixColumns

“列混淆”，AES的又一线性变换模块。直接给出对应的矩阵变换：

$M_{M} = \begin{bmatrix} 2 & 3 & 1 & 1 \\1 & 2 & 3 & 1 \\1 & 1 & 2 & 3 \\3 & 1 & 1 & 2 \end{bmatrix}$

注意此处的乘法运算依然在 $GF(2^{8})$ 下进行，在运算结果小于 $2^{8}$ 时其和通常的数乘结果一致，溢出时其处理方法有所不同（不是模 $2^{8}$）。可以参考如下实现 $GF(2^{8})$ 下乘法的Python代码，其利用“快速乘”的溢出处理逻辑：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def gmul(a,b):
    res = 0
    while b:
        if b&1:
            res ^= a
        
        a <<= 1
        if a & 0x100:
            a ^= 0x1b
        
        a &= 0xff
        b >>= 1

    return res

而在加密算法的实践中，可以发现矩阵乘法的系数只有2,3两种~~（1可以算也可以不算）~~，在部分追求高效的加密算法实践中，会选择将256个字节的乘法结果“打表”并以常量数组体现之，其理与S盒“预定义”类似。

AddRoundKey

将轮密钥和块进行逐字节加操作（在 $GF(2^{8})$ 下，等价于按字节异或；对于矩阵运算而言即为两个矩阵相加）。

宏观

AES加密时，每轮会依次进行SubBytes、ShiftRows、MixColumns、AddRoundKey四个操作（混淆-扩散-密钥），例外：
- 轮密钥RoundKey的组数比加密轮数多1，实际上RoundKey[0]就是初始密钥，第i轮调用的轮密钥是RoundKey[i]。在第一轮加密开始前，明文会先和RoundKey[0]进行一次AddRoundKey，此所谓“预白化”(pre-whitening)；
- 最后一轮加密没有MixColumns步骤。

Δ集(delta-set)及攻击过程

Δ-集和活跃位置

下述内容的参考文章：知乎 - 初探AES Square Attack，亦为笔者的square attack“入坑”之文。
~~由于小姜懒得再重新作图了，因此~~下述出现的注解性图示大量引用了该文的示意图。

考虑一个大小为256的16Bytes密文集 $c_{i}$。本密文集只有第一个字节遍历0x00到0xff，其余字节相同。
此时我们称块中 $(0,0)$ 这个位置是“活跃”(active)的。

约定若块中某位置在块集中的值不同，则该位置是“活跃”的，反之则其“不活跃”，即在块集中的值相同。
对于一个良好的加密算法/哈希函数（具备较好扩散性），对某块经过多轮加密处理后，块中的活跃位置数应逐渐增加（直至全部活跃）。

同时对于这种仅首字节（或某特定字节）完全遍历 $[0,256)$、其余字节不变的块集合为 Δ-集 (delta-set) 。

活跃位置的扩散

现在分析AES加密中，每个组件对于活跃位置扩散的影响：

注意判定活跃位置的变化时，横向观测量为仅第一个位置不同的明文块。

SubBytes：不改变活跃位置分布情况。因为SubBytes的本质是每个Byte位置自身在 $GF(2^{8})$ 下的双射，因而活跃的位置依然活跃，不活跃的位置亦然（取值一定）。
ShiftRows：行移位，其会让第 $i$ 行的活跃位置循环左移 $i$ 位，但不会增加活跃位置数。
MixColumns：列混淆，从矩阵乘法理解之较好：考虑矩阵乘法的定义，某一位置上的新值是左矩阵对应行和右矩阵对应列的内积，因此这个活跃位置会且仅会扩散到其所在行上的所有元素。
AddRoundKey：不改变活跃位置分布情况，因为对于同个密钥初始化的AES，对不同密文进行加密时轮密钥一定。

对于前两轮来说，下图能更为直观地体现活跃位置（绿块）经过不同加密步骤后的扩散情况：

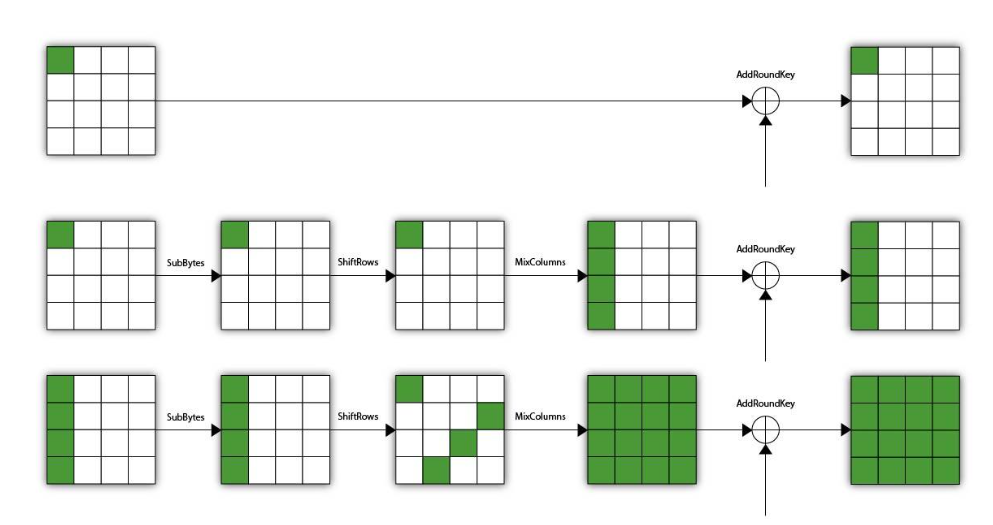
可以发现，经过两轮加密后，明文块的所有位置都已经变成“活跃”的了，即所有位置对Δ-集都能遍历0-255的所有字节。

归元

第三轮就比较有趣了：依然照葫芦画瓢式地分析，SubBytes、ShiftRows操作结束后，块(block)依然是所有位置均活跃的状态。
但MixColumns会打破这个性质（比较显然，因为无法预测某个位置是否仍能恰好遍历0-255）。

不过作为线性变换组件，MixColumns后密文块依然有一些性质可被利用。
记在一个Δ-集内，某列的第 $i$ 个字节取值为 $j$ 时，列混淆前、后的取值分别为 $x_{i,j}$、$y_{i,j}$。

显然 $i$ 的取值范围为 $[0,4)$，$j$ 的取值范围为 $[0,256)$。下述约定 $i$ 的运算在 $Z_{4}$（模4整数环）下进行；注意 $x_{i,j}$ 和 $y_{i,j}$ 的运算均在 $GF(2^{8})$ 下进行。

根据列混淆的计算式，可以推出：$y_{i,j} = 2x_{i,j} + 3x_{i+1,j} + x_{i+2,j} + x_{i+3,j}$。
继而，存在 $\sum_{j=0}^{255} y_{i,j} = 2\sum_{j=0}^{255} x_{i,j} + \cdots = 0 + 0 + 0 + 0 = 0$。

$\sum_{j=0}^{255} x_{i,j} = 0$ 这点比较显然（因为 $i$ 是活跃位置，其遍历了 $[0,256)$，自然存在其和为 $0$），其亦为表述“活跃位置”的数学方法之一。

而最后一步AddRoundKey由于只是给 $y_{i,j}$ 加上了一个常量偏移，求和后相当于对该偏移乘以256，结果依然为 $0$，即AddRoundKey并不改变这一性质（某一位置在Δ-集中的和为0）。

逆流的第四轮：借力打力

上述“归元”确实得到了某一位置在Δ-集中和为0的特性，然而第四轮加密的SubBytes作为非线性变换组件会完全破坏之。
但如此我们的分析就结束了吗？

假设我们拥有一个密文集，由于每轮的AddRoundKey实现的是按字节加，即每轮轮密钥只会影响当前块的一个特定字节，因此我们可以试着将密文“回溯”到这个性质依然成立的状态（即第三轮AddRoundKey结束后）。
此时，因为对于某一位置的密文，该位置的轮密钥正确是回溯至第三轮时Δ-集追踪其位置的密文和为0的充分条件，故可以逐个位置爆破第四轮的轮密钥，通过将密文回溯至第三轮并验证此性质是否成立，来得出轮密钥每个位置可能的值。

尽管轮密钥正确并非该性质成立的充分必要条件，但在完全选择明文攻击中，攻击者可以构造多组Δ-集，对爆破的每一位密钥的可能值取交集，可以极快地锁定密钥（笔者测试多数情况下2组Δ-集有极大把握可以唯一确定轮密钥，~~数学分析什么的就先咕着~~）。
即使只有一组Δ-集，测试表明轮密钥的可能取值组合也不会太多（记 $c_{i}$ 为第 $i$ 位的轮密钥可能取值，可能组合数显然为 $\sum_{i=1}^{16} c_{i}$，但实践中多数的 $c_{i} $ 取值均为1，可能密钥数一般在 $10^{4}$ 的数量级左右），其后再通过完整解密校验等方式亦极易得出正确密钥。

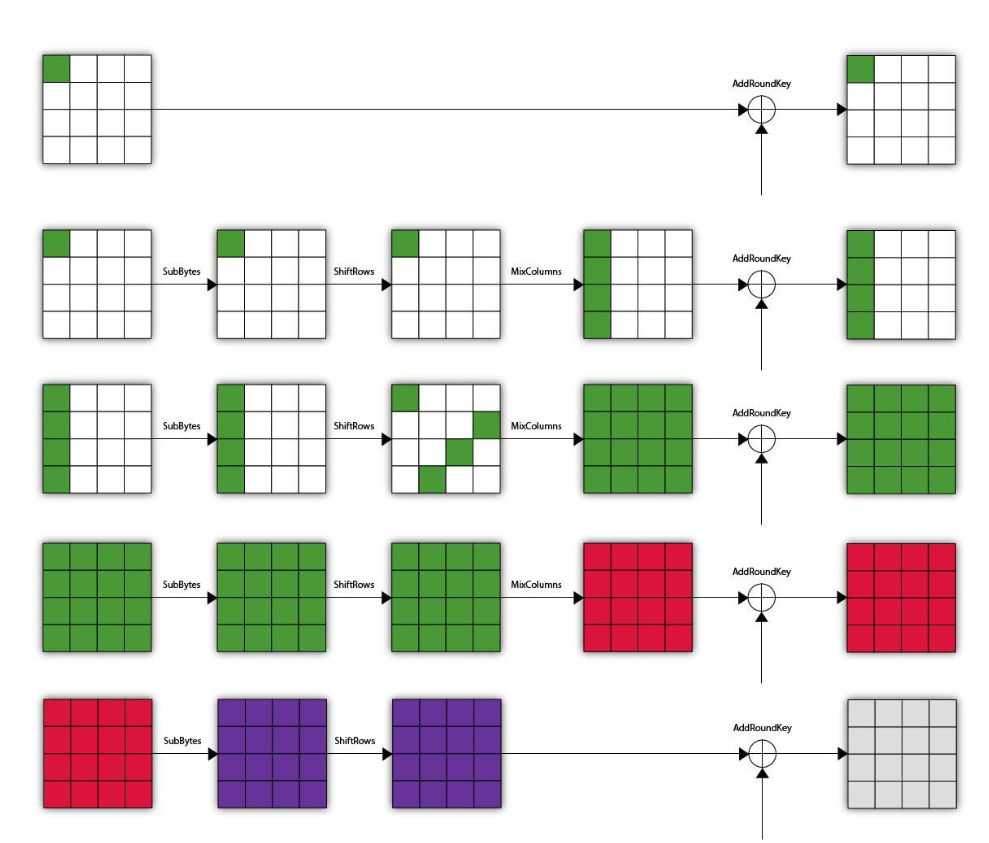
下附前四轮加密中位置特性变化的示意图，以便理解：

白色：非活跃位置，该位置在同一状态的Δ-集中是定值；
绿色：活跃位置，该位置在同一状态的Δ-集中遍历了0-255的所有字节；
红色：“归元”特性，该位置在同一状态的Δ-集中值求和为0；
紫色：未知，该位置没有特殊性质。

上述说明的“同一状态”对充分理解积分攻击非常关键。

参考代码

欢迎关注Hibiscus在github上的AES-Integrals项目鸭a.a：github - AES-Integrals

Python

inv_s_box = (82, 9, 106, 213, 48, 54, 165, 56, 191, 64, 163, 158, 129, 243, 215, 251, 124, 227, 57, 130, 155, 47, 255, 135, 52, 142, 67, 68, 196, 222, 233, 203, 84, 123, 148, 50, 166, 194, 35, 61, 238, 76, 149, 11, 66, 250, 195, 78, 8, 46, 161, 102, 40, 217, 36, 178, 118, 91, 162, 73, 109, 139, 209, 37, 114, 248, 246, 100, 134, 104, 152, 22, 212, 164, 92, 204, 93, 101, 182, 146, 108, 112, 72, 80, 253, 237, 185, 218, 94, 21, 70, 87, 167, 141, 157, 132, 144, 216, 171, 0, 140, 188, 211, 10, 247, 228, 88, 5, 184, 179, 69, 6, 208, 44, 30, 143, 202, 63, 15, 2, 193, 175, 189, 3, 1, 19, 138, 107, 58, 145, 17, 65, 79, 103, 220, 234, 151, 242, 207, 206, 240, 180, 230, 115, 150, 172, 116, 34, 231, 173, 53, 133, 226, 249, 55, 232, 28, 117, 223, 110, 71, 241, 26, 113, 29, 41, 197, 137, 111, 183, 98, 14, 170, 24, 190, 27, 252, 86, 62, 75, 198, 210, 121, 32, 154, 219, 192, 254, 120, 205, 90, 244, 31, 221, 168, 51, 136, 7, 199, 49, 177, 18, 16, 89, 39, 128, 236, 95, 96, 81, 127, 169, 25, 181, 74, 13, 45, 229, 122, 159, 147, 201, 156, 239, 160, 224, 59, 77, 174, 42, 245, 176, 200, 235, 187, 60, 131, 83, 153, 97, 23, 43, 4, 126, 186, 119, 214, 38, 225, 105, 20, 99, 85, 33, 12, 125)

inv_shift_row_idx = (0,13,10,7,
                    4,1,14,11,
                    8,5,2,15,
                    12,9,6,3)

def bytes_xor(a:bytes,b:bytes):
    return bytes([i^j for i,j in zip(a,b)])

def inv_shift_rows(a:bytes):
    return bytes([a[inv_shift_row_idx[i]] for i in range(16)])

def inv_sub_bytes(a:bytes):
    return bytes([inv_s_box[i] for i in a])

def atk(ciphers:list[list[bytes]]):
    result = [[] for _ in range(16)]

    for cipher in ciphers:
        assert len(cipher) == 256, "Delta-set required to conduct the integral attack"

        trykey = bytes(16)
        
        tempopt = []
        for idx in range(16):
            keyidx = inv_shift_row_idx[idx]
            for i in range(256):
                trykey[keyidx] = i
                sumval = 0

                for bk in cipher:
                    bk = bytes_xor(bk,trykey)
                    bk = inv_shift_rows(bk)
                    bk = inv_sub_bytes(bk)
                    sumval ^= bk[idx]

                if sumval == 0:
                    tempopt.append(i)        

        result[keyidx] = list(set(tempopt) & set(result[keyidx]))
    
    return result

C++

因考虑了预留扩展攻击接口、类型安全、编译链接、可维护性与可读性等问题，下述实现不是最简攻击代码，亦不是效率最极限的代码~~毕竟还没有上什么手搓set呀，多线程呀之类的极限操作~~。
但依然架不住运行效率极高（以最佳优化方式编译，三组 delta-set 在笔者搭载 Intel i7-13700H CPU的笔记本上的密钥破解耗时小于100ms）。

考虑篇幅因素，此处仅给出关键代码（比如Attack_Interface等实现未给出），完整代码可以移步上述的AES-Integrals项目获取~~欢迎乱叉(fork)~~。

namespace atk4_1
{
    class Attack
    {
        using ciphertexts = std::vector<block>;
        using ciphertext_rvw = std::span<const block>;
        using keyls = std::array<std::unordered_set<byte>, 16>;

    public:
        constexpr Attack() :copy{}
        {

        }

        constexpr Attack(const Attack&) = delete;
        constexpr Attack& operator=(const Attack&) = delete;

        constexpr void append_ciphertexts(ciphertext_rvw vw)
        {
            if (vw.size() != 256)
            {
                throw std::invalid_argument{"Each group of ciphertext must be a delta-set of length 256"};
            }
            copy.push_back({ std::from_range,vw });
        }

        void solve()
        {
            if (copy.empty())
            {
                throw std::runtime_error{ "No ciphertexts provided yet!" };
            }

            for (ciphertext_rvw v: copy)
            {
                if (!status)
                {
                    status = verify(v);
                }
                else
                {
                    auto temp = verify(v);
                    for (auto&& [s1,s2] : std::views::zip(*status,temp))
                    {
                        for (byte i : s1)
                        {
                            if (!s2.contains(i))
                            {
                                s1.erase(i);
                            }
                        }
                    }
                }
            }

            if (std::ranges::all_of(*status, [](auto x) {return x == 1;}, &std::unordered_set<byte>::size)) //Only key combination possible
            {
                std::println("Key resolved:");
                for (const auto& i : *status)
                {
                    for (auto t : i)
                    {
                        std::print("{}", t);
                    }
                }
                std::println();
            }
        }
    private:
        constexpr keyls verify(ciphertext_rvw vw) const
        {
            keyls ret;
            block sample_key;

            for (auto idx : std::views::iota(0, 16))
            {
                uc keyidx = Attack_Interface::inv_shift_rows_idx[idx];
                //Checking at index 0-15 through the ciphertexts rewinded to round 3
                //Keys that await to be enumerated should be forward-mapped to round 4(the keys trying to ...

                for (auto i : Attack_Interface::iota_byte)
                {
                    sample_key[keyidx] = i;
                    uc sumval = 0;
                    for (block bk : vw)
                    {
                        Attack_Interface::bytes_xor(bk, sample_key); //AddRoundKey
                        Attack_Interface::inv_shift_rows(bk);
                        Attack_Interface::inv_sub_bytes(bk);

                        sumval ^= bk[idx];
                    }

                    if (sumval == 0)
                    {
                        ret[keyidx].insert(i);
                    }
                }
            }
            
            return ret;
        }
        
        std::vector<ciphertexts> copy;
        std::optional<keyls> status;
    };

    void atk4_1::test_atk4_1()
    {
        using group_t = std::array<block, 256>; //delta-set

        Func_Timer t;
        std::string str{};

        auto key = block_fromhex(str).value_or(block{});
        auto aes = AES<4>(key);

        std::println("4th round key:\n{}", aes.output_rk4());

        Attack atk{};
        block sample{};
        group_t ciphers{};

        for (auto q : Attack_Interface::iota_byte | std::views::take(2))
        {
            sample[15] = byte(q);

            for (auto i : Attack_Interface::iota_byte)
            {
                sample[0] = byte(i);
                ciphers[i] = aes.encrypt(sample);
            }
            atk.append_ciphertexts(ciphers);
        }

        atk.solve();

    }
}

!...?

靶子

假设存在这样一个非常有趣的加密系统：


def what():
    aes = AES.new(key,round = 4) #AES is custom-defined class enabling round designation
    
    while True:
        lucky = urandom(1)
        print(f'[+] Today my lucky byte is:{lucky.hex()}')
        print(f'[+] And the ciphertext is: {aes.encrypt(pad(lucky)).hex()}')
        if input('[-] Still want more interactions(y/[n])?') != 'y':
            break

实际上类似于这种加密系统的应用颇为广泛——对一个固定前缀（或后缀）加上少量的“活跃”字节进行加密。
对于形如上文的加密系统，我们只需与之不断交互，直至能获取到一个Δ-集所对应的密文，即可展开AES积分攻击，破解轮密钥。

能不能再给力一点？

上述我们讨论了当我们能够获得一个（最好是多个）delta-set 时的攻击方法。那么，假如受制于攻击条件等（如上述的加密Orcale只给了100次“随机”加密机会，最终获得的不同密文甚至可能只有60-70个），无法获得这样的 delta-set 呢？